BCH upgrade proposal: Use ASERT as the new DAA
Abstract
The current BCH difficulty adjustment algorithm (DAA) allows for a switch miner to extract a large amount of profit from constant-hashrate miners. This strongly discourages constant-hashrate mining and encourages switch mining, and causes oscillations in difficulty and hashrate. In my test simulation, the stolen profit is on the order of 6% lost revenue by constant hashrate miners for the current DAA, but only about 0.35% to 0.65% for the EMA family of DAAs. I propose a specific type of EMA, called ASERT, for BCH to be activated in the November 2020 scheduled protocol upgrade, and provide extensive simulation results on this algorithm, as well as an untested sample C++ implementation.
Why the DAA is a problem
The current BCH difficulty adjustment algorithm — known as cw-144, since the algorithm is based on chainwork — has a problem: it is prone to oscillation. This oscillation is the result of the current BCH DAA using a simple moving average, and has been described in detail in previous works. It was a known issue with cw-144 even in October, 2017, before it was activated on mainnet.
(If you're already familiar with this oscillation, such as if you watched my Feb 27, 2020 video, feel free to skip this section and jump to the Stable DAAs heading.)
There are a few reasons why this bug, and the incentive problem it engenders, are problematic:
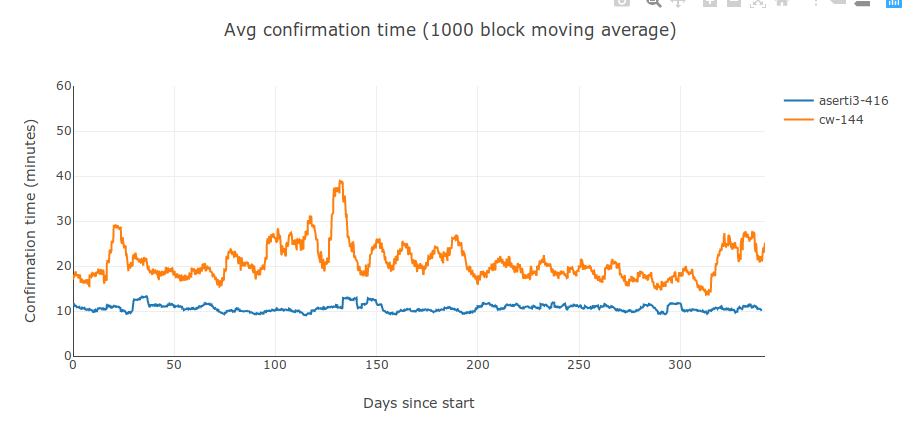
It increases average transaction confirmation times by a factor of about 2x if 90% of the hashrate behaves in a rational manner;
It causes the chain to stall completely if 100% of the hashrate behaves in a rational manner;
It allows for some really nasty selfish mining attacks. Selfish mining attacks cause block reorgs, and reduce public confidence in the block chain, and make double-spend attacks more feasible;
It punishes miners for being loyal to BCH;
It punishes small solo miners who do not have the technological sophistication to automate hashrate switching strategies; and
It allows for malicious strategies in which a miner can intentionally amplify the oscillations and pro-switching incentives, either by switching their hashrate themselves in a pumped fashion, or by manipulating the timestamps of the blocks they mine.
In brief, the oscillation is due to cw-144 using a simple moving average (SMA) over the last 144 blocks to estimate hashrate. When e.g. a high-hashrate block leaves the SMA window, it reduces the difficulty by the same magnitude as a new block entering the window would increase it. Blocks leaving the window therefore sharply change the difficulty in a direction that incentivizes miners to repeat the hashrate of the departing block. I call this effect "hashrate echoes." Notably, these echoes do not require any malicious miner behavior to occur. They are merely the result of miners following the direct short-term incentives that the DAA gives them.
These hashrate oscillations have a period of about 1.05 days, so they're not visible on most difficulty or hashrate charts (which use a 1-day sample interval), but they're clearly visible on this interactive chart.
These hashrate echoes first appeared in BCH shortly after the cw-144 DAA was activated on November 2017. At that time, the oscillation amplitude was about 1 EH/s, with daily peak hashrate typically at 2x the daily minimum:

Due to changes in the behavior of a few large BCH mining pools, these echoes became significantly more severe around October 1st, 2019, prompting an article from BitMEX Research. The oscillation amplitude reached 11 EH/s, with daily peaks at 4x to 8x the daily minimum. Similar extremes were observed around January 20, 2020 and most of April, 2020.

These oscillations in hashrate cause and are caused by changes in mining difficulty. These difficulty oscillations frequently exceed 10% in amplitude, causing dedicated miners to mine at a loss (compared to mining BTC) most of the time, with switch miners swooping in for around 2-6 hours per day to capture all of the profitable blocks.
These oscillations significantly worsen the user experience. The high-hashrate bursts are short; the hashrate droughts in between are long. Most transactions are issued during hashrate droughts, and the average transaction needs to wait much longer than the ideal 600 seconds for the normal Poisson block distribution. This effect can be seen in this interactive chart of confirmation times. Confirmation times have also gotten worse recently, averaging about 15 minutes since September, 2019, and peaking at 28 minutes in January, 2020.

In Sep-Oct 2017, kyuupichan and a few other developers wrote the "difficulty" software suite to simulate these difficulty oscillations and hashrate switching with different DAAs. In Feb 2020, I extended this suite with a graphing browser-based UI (code; slow online version). These simulations confirmed that with the cw-144 algorithm, these oscillations are produced without any malicious miner behavior. All that is necessary to generate them with cw-144 is for miners to mine whichever coin (BCH or BTC) is the most profitable at any given moment.

The simulations also prove that the oscillations are specifically cw-*'s fault. The oscillations are present in all variants of the cw family when miners follow rational incentives, with larger and more frequent oscillations for cw variants with higher sensitivity (e.g. cw-144 is worse than cw-576), but the oscillations are entirely absent from all other good DAA families, regardless of sensitivity.

The fact that it's possible for switch miners to earn 5-20% more than constant-HR miners is a bug. This bug is the result of the 1-day resonance and tendency for oscillation that the current DAA has. We can reduce the incentive for switch mining by about 90%-95% by switching to a different DAA, such as an EMA-family algorithm.
Stable DAAs
The instability in the simple-moving-average (SMA)-based cw-144 algorithm is caused by the influence of a block on difficulty ending abruptly when the block leaves the 144-block window. This instability can be avoided by having the influence of a block fade slowly over time. For example, if the influence fades linearly over 144 blocks, the instability disappears. This is what the lwma (linearly-weighted moving average) algorithm does, as well as Tom Harding's related wt (weighted time) algorithm. Another option is to have the influence fade exponentially over time, with e.g. a 144-block time constant. This is what the EMA (exponential moving average) family of algorithms do. This family includes many variants, such as Jacob Eliosoff's ema-1d and simpexp-1d, Tom Harding's wtema, and Mark Lundeberg's asert algorithms.
Among these stable DAAs, we identified four major candidate algorithms: asert, wtema, lwma, and wt. All four algorithms performed well in my simulations and in zawy12's simulations. Below is a table of data on one such simulation run for all four candidate algorithms, plus cw for reference, at three different responsiveness settings corresponding to 1 day (as in the current DAA, cw-144), 2 days, or 4 days. The table includes the average confirmation time for transactions in the third column. That number should ideally be as low as possible. In the "Greedy" through "Steady" columns, the table shows the relative profitability of various mining strategies (compared to mining BTC). In the final column, the table shows the advantage to be gained by switching from the worst mining strategy to the best mining strategy. That number should ideally be as close to 0% as possible.

cw-144, performs the worst of all algorithms tested by a large margin. The best DAA in this test, asert-576 only took 51% as long to confirm the average transaction, and reduced the incentive for switch mining by 94.4% compared to cw-144. All algorithms except cw clustered closely together in performance at a given responsiveness setting. The performance advantage for the longest responsiveness (576 blocks, 4 days) was modest compared to the middle setting.Differences in hashrate regulation performance between these four options in simulations were minor. There seemed to often be a small edge for the EMA based algorithms (wtema and asert), but the advantages were small enough that we believed that the choice should be made on other concerns, like implementation complexity. Both lwma and wt require sampling every block header in their windows (e.g. 288 blocks) in order to calculate the next block's difficulty, whereas the EMA family generally only requires sampling two block headers, so our attention focused on the EMA family.
Our attention then focused on determining which EMA algorithm to use. The most interesting ones seemed to be wtema and asert.
WTEMA and ASERT
The two EMAs that seemed like the best candidates were wtema and asert. The wtema algorithm was created by dgenr8 (Tom Harding) on or before Jan 1st, 2018. It is an exceptionally simple integer-only EMA based on the following pseudocode:
next_target = prior_target / (IDEAL_BLOCK_TIME * alpha_recip)
next_target *= block_time + IDEAL_BLOCK_TIME * (alpha_recip - 1)In abstract terms, it first estimates how much the block's "target" (the reciprocal of difficulty) should be changed in order to achieve 600 second blocks if the most recent block interval were perfectly representative of the hashrate. Then, it performs a weighted average between that value and the last block's target, using 1/alpha_recip as the weighting coefficient. This makes wtema a recursively defined function, and a classic example of a simple first-order IIR filter, equivalent to an electronic RC filter. But don't be fooled by the simplicity: it performs just as well as a complex PID controller system, but with a fraction of the complexity.
The asert algorithm was developed mostly by Mark Lundeberg on or before February, 2020, though an equivalent formula was also independently discovered in 2018 by Jacob Eliosoff but without Mark Lundeberg's detailed analysis, and again in 2020 by Werner et. al at Imperial College London. asert is defined by the following formulae:
target_timestamp = (height + 1 - activation_height)*IDEAL_BLOCK_TIME
next_target = target_at_activation * 2^((last_timestamp − target_timestamp)/tau)Note: ^ denotes floating point exponentiation, not integer XOR.
asert stands for absolutely scheduled exponentially rising targets. In abstract terms, asert works by defining an ideal block schedule, and setting each block's difficulty exponentially, based on how far ahead of or behind that schedule its parent block was. For every tau seconds ahead of schedule a block is, the next block's difficulty goes up by a factor of 2. Reasonable values of tau can be from a few hours to a few weeks. Like wtema, asert's code and math are simple, and only depend on two blocks. Unlike wtema, asert depends only on the most recent block and the genesis block or the fork block at which asert was activated. This avoids the recursive definition that wtema has. For more information on asert, I highly recommend Mark Lundeberg's succinct introductory paper.
The two algorithms are functionally nearly identical when block intervals are reasonably close to normal, and only differ at the extremes.

The debate between the two algorithms seemed to center around four issues:
Integer approximations — easier with
wtemathanasert, due toasert's use of an explicit exponential function, but possible in bothSingularity and negative solvetimes — problematic with
wtema, but notasert, as shown in the graph above (source: dgenr8).wtemalikely needs rules restricting solvetimes to be greater than some value (e.g. >-0.5 * 144 * 600 secforwtema-144)Mathematical and theoretical elegance — good with both, but better for
asertAccumulation of rounding/approximation error — modest in
wtema, but absent inasertdue to its absolute nature
The main issues seemed to be #1 and #2. The need for integer approximations of 2^x makes asert more complex. The need to protect against large negative solvetimes makes wtema more complex. Ultimately, we decided that it would be better to add a few lines of code to the difficulty calculation function itself than to add or change other consensus rules in order to forbid large negative solvetimes, so we settled on asert.
It is important to not include floating point code in Bitcoin consensus rules, since C and C++ are generally not IEEE 754-compliant, and different compilers and hardware can disagree on floating-point computations. So we need an integer approximation. We then began looking at different approximation implementations.
The method I chose relies uses the 2^x = 2 * 2^(x-1) identity to shift the 2^x approximation to the 0 <= x < 1 range. Once this has been done, asert becomes remarkably insensitive to any residual error, and even an approximation as simple as 2^x ~= 1 + x works pretty well. But we could do much better than that, so we did. After testing a few approaches, I eventually choose to use Mark Lundeberg's cubic approximation of 2^x for 0 <= x < 1. This approximation maintains an error margin below 0.013%.

Here is an as-yet untested example C++ implementation of the aserti3 algorithm, and here is a well-tested python3 implementation of aserti3. Performance mirrors that of true asert very closely. Testing of the C++ implementation should follow soon.
The main competing approximation option was Jacob Eliosoff's exp_int_approx() implementation, which uses an algorithm grabbed from Stack Overflow to achieve arbitrary precision, but at the cost of the use of a for loop and more opaque math and code.
I chose a half-life of 2 days (tau = 2*24*60*60, equivalent to a responsiveness setting of 2*144/ln(2) or aserti3-415.5 due to a difference in exponential bases) because that seems within the range of values that perform near-optimally in simulation while also being easy for humans to understand and discuss — for every 2 days ahead of schedule a block's timestamp gets, difficulty doubles. I consider a half-life of 1 day (aserti3-207.75) to also be acceptable. I recommend against going lower than 207.75 or higher than 576.
Activation
Because the asert calculation depends on the fork block's height and difficulty, implementation is substantially simpler and easier if activation is on a predetermined block height, rather than at a predetermined median time past (MTP). If the latter approach is used, then post-fork the new asert code will need to search the blockchain for the first block whose MTP exceeded the fork time, and extract the height and difficulty from that block's header. In contrast, if a fork height is used, the asert algorithm just needs to search the blockchain for the difficulty at the known height — a considerably simpler operation. While an MTP-based activation of asert is possible, it is my belief that it will be simpler and better overall to do this activation based on block height instead.
Bitcoin ABC has a tradition of adding a poison pill to their code in advance to fork off obsolete versions of their software at a predetermined MTP. If a fork height is used to activate asert, then the poison pill activation and the asert activation will not coincide exactly. This will likely result in two technical hard forks in quick succession, rather than a single three-way fork. This is a minor disadvantage to using a fork height activation. But even if the poison pill does not coincide perfectly, it will still serve its purpose: It will discourage individuals from continuing to run obsolete software.
I believe that the (potentially permanently) simpler code of a height-based activation of asert outweighs the timing mismatch issue, so I used a height-based activation in my sample C++ implementation. I am okay with this being changed if a majority of the BCH development community disagrees.
Testnet
The standard 20-minute testnet rule applies: A block may be mined with difficulty 1 if its timestamp is at least 20 minutes ahead of the previous block's. Because asert difficulty adjustments are based on time rather than block height, the "timewarp" technique to reset difficulty on testnet (by jumping the timestamp forward repeatedly to lower the average chainwork over the last difficulty adjustment interval) does not work. Because of this, testnet difficulties will be slower to adjust after this change than before, and testnet users may be stuck with 20 minute blocks for a few days after an ASIC miner leaves testnet. This could be addressed by reducing the tau value on testnet, but the cost of this change would be that testnet would less accurately resemble mainnet. Developers who use testnet frequently should discuss which approach they prefer.
Attacks
We have looked at a few different types of attack against aserti3, and so far, with existing consensus rules and non-ABC/BCHN node policy, aserti3 outperforms cw-144 in almost all scenarios. There are only a few that seem concerning. All attacks that have been identified so far are small in magnitude (usually smaller than other known and existing attack vectors) and/or easily mitigated with small node policy changes.
The attack scenarios of significant concern are all ones that the current DAA protects against by using a median-of-three prefilter. The current DAA will use the median timestamp of the most recent three blocks as well as the median timestamp of the blocks 144, 145, and 146 blocks ago. This median-of-three prefilter effectively adds 1 block of delay to the DAA in most scenarios, which prevents difficulty from being exploited in a 2-block reorg attack, such as are used in most known selfish mining strategies. However, this extra block of delay also tends to cause oscillation issues in most DAAs that aren't already oscillatory, including EMAs, so zawy12 and I strongly advise against the use of median prefilters. This leaves two types of 2-block attacks as needing special attention.

The first attack is selfish mining in the absence of oscillations. In this scenario, a selfish miner A can make a block A1 with an artificially early timestamp — say, a solvetime of 1 second — which increases the difficulty of the next block A2 by 0.24%. This can cause chain A2 to have slightly more chainwork than B2, and can make nodes to prefer A2 over B2 even if B2 was seen first. Bitcoin ABC and BCHN already have node policy rules that block this attack, but Bitcoin Unlimited and most other nodes do not. To address this issue, we recommend that all remaining nodes add hysteresis to the first-seen rule for blocks: nodes should only switch chains if the new chain's work exceeds the first's by some substantial threshold, like 10% or 50% of one block's chainwork.
The second attack is the FTL (future time limit) attack. In this attack, a miner creates a block with the timestamp set to the FTL (currently 7200 seconds in the future according to most BCH nodes' policies) to lower the difficulty on a secret chain, then mines as many blocks as possible until the difficulty on that chain returns to normal. This attack can be slightly more effective for asert than for cw in some (but not all) circumstances because asert's difficulty responds after a single block rather than two for cw. This effect is largely mitigated by the use of a slower responsiveness setting (aserti3-2d is about 1/4 as responsive as cw-144), but it is better addressed by simply lowering the FTL.
Lowering FTL appears to be a straightforward improvement. Many altcoins have lowered FTL with no observed negative consequences. In the modern world of NTP and GPS, keeping system clocks synchronized to within 0.1 sec is easy, so there's no reason to allow up to 7,200 sec errors without punishment. Even in humanity's interplanetary future, an FTL of 600 seconds will not cause problems for the Bitcoin protocol, because blocks in which the timestamp reflects the publication time will result in blocks being received with old timestamps on other planets, not future timestamps. In the far future, once bitcoin mining starts to be performed on vehicles traveling at relativistic speeds, we might have to rethink the FTL; but until then, I recommend lowering it to 600 seconds or less. Furthermore, whenever the FTL is reduced, the DEFAULT_MAX_TIME_ADJUSTMENT limit on how far peer time can differ from local time (the "peer time revert rule", as zawy12 calls it) must be adjusted accordingly.
This is not an exhaustive discussion of potential attacks, but merely an introduction to the known attacks of concern. Discussion of a few other attack scenarios can be found in zawy12's EMA for BCH (part 2) and Hash Attack Examples Github issue threads.
Conclusion
The current DAA, cw-144, is causing a lot of problems for BCH. We should fix it. Switching to an EMA or LWMA algorithm would fix those problems. The aserti3-2d algorithm appears to be far superior to cw-144 overall, and I believe it to be the best option we have.
A good DAA should have the following properties, in rough order of importance:
It should be stable, and not prone to oscillations;
It should keep confirmation times low;
It should keep incentives for miners to perform hashrate shenanigans low;
It should keep incentives for miners to perform timestamp manipulation shenanigans low;
It should keep incentives for miners to perform selfish mining shenanigans low;
Because of #3, #4, and #5, honest mining strategies with steady hashrate should get near-optimal income;
The chain should recover quickly after sudden changes in hashrate and/or exchange rate;
The average block interval should be kept close to the target (e.g. 600 seconds);
The algorithm should be mathematically simple and elegant;
The algorithm should be easily understood and analyzed;
The algorithm should be easy to implement elegantly and simply; and
The algorithm should have few or no edge and corner cases.
In this article, I have provided some evidence that aserti3-2d likely satisfies most or all of these requirements. I encourage the BCH developer community, and the BCH community as a whole, to search for scenarios in which aserti3-2d fails to satisfy these criteria, and to compare aserti3-2d to cw-144 and any other candidate DAAs in those scenarios.









This is very helpful and informative article. Thanks for this my friend.