What is CashFusion?
CashFusion is an anonymity technology for Bitcoin Cash currently in alpha testing. It lets people mix coins anonymously and trustlessly. Unlike usual mixer services - there's no trace of who got how much in and who got how much out.
So, even if a CashFusion server is busted or undercover agents are listening on the network - there's no chance to be deanonymized.
As you know Bitcoin Cash's blockchain is a public ledger (like many other blockchains).
For example we can know that someone, let's name her Alice, has currently 1 satoshi.
We don't know who Alice is, but if she sends this satoshi to an exchange and reveals the identity - suddenly you know who she is and you can see all her previous operations. Also, you can trace other people who she interacted with.
This is called "chain analysis".
How can poor Alice hide from the prying eyes? She needs help.
So, Bob comes to help.
Two people come into a room. Alice has 1 satoshi in one hand and 3 satoshis in the other. Bob has 2 satoshis in one hand and 4 satoshis in the other.
Something happens inside.
Two people in black robes come out of the room. One has 3 satoshis and another one has 4 satoshis. We don't know who of them is Alice and who is Bob.

Can we try to guess who is who?
So, what happened inside? CashFusion!
Alice took her 1 satoshi and 3 satoshis and have put it on a table as 4 identical satoshis. Bob did the same with 2 and 4 satoshis. In total, there were 1+3+2+4=10 identical satoshis on the table. Anyone can take any amount, but less than they brought in. Now, Alice takes 3 satoshis, Bob takes 4 satoshis and leave the room.
3 satoshis that are left on the table are taken by a Bitcoin Cash miner to process this transaction.
(In reality nobody put anything on any table, it was just math)
Alice: 1 + 3 = 3 (+1 to the miner)
Bob: 2 + 4 = 4 (+2 to the miner)
Note that "3 satoshis" that Alice takes out are not the same "3 satoshis" that Alice brought in - they were divided and mixed with others and "fused" back again, so they are not linked in any way. I didn't think about this coincidence until after it was a bit too late, but the second example should be more clear. Same with Bob - just a coincidence.
What do we see on the blockchain?

Nice, huh? We don't even know if Person 1 and 2 are the same person.
Even if we somehow knew that 1 sat and 3 sat previously belonged to Alice - we can't know whether Alice is now Person 1 or Person 2.
It could be that Alice took 1+3=4 satoshis, paid the miner nothing and left with 4 satoshis. But it's totally possible otherwise (which is correct) that she brought 1+3, gave miner 1 satoshi and left with 3. (In reality, of course, you must pay miners fee)
This is a simple example. Let's get a bit more complex.
Charlie joins the room and they do the following:
Alice: 2 + 8 = 10 = 9 + (1 to a miner)
Bob: 7 + 5 + 3 = 15 = 5 + 8 + (2 to a miner)
Charlie: 7 + 2 = 9 = 7 + (2 to a miner)Notice that Bob does a clever thing. He brings in 7, 5 and 3 satoshis, but leaves as "two people", each holding 5 and 8 satoshis respectively.
So, suddenly we have this on the blockchain:
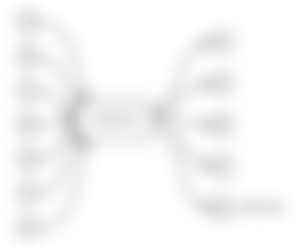
Looking just at this: how many people participated? What did everyone do?
From the looks of it, it might have been four people, who took 9, 5, 8 and 7 satoshis each.
But, really it was three, because Bob got outside with 5 and 8, looking like two people.
Just looking at the transaction - we can tell that it's plausible that one to four people participated.
But we can't tell who is who here, can we?
Let's ask our good friend computer to help us. We will try all possible combinations and see what we get.
At first we can try to deanonymize any random person (Alice) and see what possible thing could she have done.
8 - 5 = 3 → It's possible that Alice got in with 8 satoshis and got out with 5 satoshis and left 3 satoshis to the miner. Yep.
8 - 7 = 1 → Put in 8, got out with 7, leaving 1 satoshi. Yep.
7 - 5 = 2 → Put in 7, got out with 5, leaving 2. Yep.
7+7 - 5-8 = 1 → Went in with 7 and 7 (14), got out with 5 and 8 (13), leaving 1 satoshi to the miner. Yep, plausible.
So, we've got a few plausible combinations. How many more are there?
7 - 5 = 2
7 - 5 = 2
2+8 - 9 = 1
...
7+2 - 8 = 1
7+2 - 7 = 2
5+3 - 5 = 3
5+3 - 7 = 1
...
2+8+5 - 9-5 = 1
2+8+5 - 5-8 = 2
2+8+5 - 5-7 = 3
2+8+3 - 5-7 = 1
...
8+3+7 - 9-8 = 1
8+3+7 - 9-7 = 2
8+3+7 - 8-7 = 3
8+3+2 - 5-7 = 1
8+7+2 - 9-5 = 3
8+7+2 - 9-7 = 1
...
2+8+7+5 - 9-5-7 = 1
2+8+7+5 - 5-8-7 = 2
2+8+7+3 - 9-8 = 3
2+8+7+7 - 9-5-8 = 2
2+8+7+7 - 9-5-7 = 3
...
2+8+7+5+7+2 - 9-5-8-7 = 2
2+8+5+3+7+2 - 9-8-7 = 3
2+7+5+3+7+2 - 9-8-7 = 2
8+7+5+3+7+2 - 9-5-8-7 = 3What? How many were there?
231 possible combinations!
So, now to deanonymize the second person - we need to take each of these as a guess and see how many possible combinations left for each of these cases.
But still, 231 combinations for a first try isn't that bad.
Let's look at a real example. This is a real CashFusion transaction: 9e28..887.
Here are the inputs and outputs in satoshis (truncated):

The miner got 16342 satoshis. The transaction has 111 inputs ("people" getting in) and 17 outputs ("people" getting out).
It seems like these numbers would be easier to deanonymize, since they look like not many of those inputs would add up to some outputs, leaving less than 16342 satoshis to a miner...
When we try to run our tester that generated all of the previous outputs - it starts giving theories slowly, like this:
21348863 - 9538973-11802770 = 7120
# got in with 21348863 sat, got out with 9538973 sat and 11802770 sat,
# leaving 7120 sats to a miner
52741370 - 11802770-18998471-21932001 = 8128
85075026 - 937750-21932001-25985765-36204143 = 15367... but then it gets stuck. What happened?
To explain it, we need to try a simpler example first.
Let's try a much simpler transaction. I've generated a similar transaction, where only 3 players, just like before (Alice, Bob and Charlie) have participated with unique enough sums, that seem like the ones from the real transaction.
inputs = [827625, 311935, 219481, 305525, 438511, 644967, 515276]
outputs = [663392, 474748, 1607187, 514230]
the miner got 3763If we run our program - it seems OK, it gives out that indeed, despite there being crazy amounts - there are only 6 plausible ways to combine them that are consistent with what the miner got.
Only 6 things that the first person could have done.
That's much lower than our original 231, so it seems that our theory about more unique numbers being easier to deanonymize holds.
But is it?
What we're looking at is "7 inputs and 4 outputs" and we get 6 plausible explanations almost instantly.
Let's bump it up!
10 inputs, 5 outputs. 4 players. Instant. 16 plausible combinations.
14 inputs, 8 outputs. 5 players. About 1 second. 71 plausible combinations.
17 inputs, 9 outputs. 6 players. 19 seconds. 860 plausible combinations.
Note that the program is written in Go language, so it's pretty close to what the computer can achieve. It's fast. Yet it takes 19 seconds to get through all possibilities.
7 players. 18 inputs, 11 outputs. 2 minutes! 7859 plausible combinations.
Ouch! Now that's getting slow.
If we try to chart how long our experiments take, considering how many inputs and outputs go into the transaction:

The time just skyrockets. 150 seconds is 2.5 minutes! Each next input and output is going to be even slower.
So, back to our transaction with 111 inputs and 17 outputs. How much time would we need to get all plausible combinations that might be what person one did?
I've measured how fast my computer can try out random combinations - it turns out that it can test about 53 million combinations per minute.
How many tries do we need?
That's where we go into crazy numbers. We need to try about 2*2*2*2*2....(repeat this 111+17=128 times) combinations - it's a very big number, it has 38 zeroes in it!
To imagine that number - imagine all the stars of our galaxy (Milky Way), now imagine each grain of sand on each of these stars... wow, right? Now multiply that by 1 billion! That's how many tries we need to do to go through all of the possible combinations to find all things that person one could have done. (Source)
So, at the speed of 53 million tries per minute... lets take all the computers in the world (about 2 billion) and ask them to try these combinations. Now, just to be safe - we'll start building computers and won't stop until we create 100 000 times more computers and ask them to join us too. 100 000 times more than there are computers in the World. Surely, we're going to end this computation fast...
Alas, it would take us 61 billion years.... or about 4 times longer than the universe has existed. Just to try all possible combinations for person one.
Ok... maybe there are some optimizations that would allow us to cut the whole huge chunks of data and we can somehow end it up in some reasonable time...
Well, we will still need to find all the plausible combinations and try them out. Would we be able to even store them? Somewhere?
Let's see at how many combinations are there, just like we looked at the time:

Oh, no...
You see where this is going, right?
I've asked my computer to try random guesses from these 111 inputs and 17 outputs to estimate how many plausible results there would be. In about 1 minute, my computer found 1723 plausible combinations out of 53616189 possibilities it tried. So, each minute that my computer works - it would find 1723 more combinations.
Remember these 100 000 times the number of computers in the World? They will be finding 1723 combinations per minute per each computer for the next 61 billion years.
This is just to find all the possible things that person one did in that transaction.
In total all these computers after 61 billion years would find about 10 000 000 000 000 000 000 000 000 000 000 000 possible things that person one did.
Here's the problem. After we're done with that, we would need to take first of this unimaginable number of combinations and then spend about 6 more billion years trying to figure out all plausible combinations of what person two did assuming person one did that first thing... then about 600 million years for person three... then... then.. then... after we have finally found some billions or trillions of plausible explanations for what all people did, we would move to second number, with 9 999 999 999 999 999 999 999 999 999 999 998 left, each taking probably about 7 billion years to finish.
Even if we try to do "depth-first" search - i.e. as soon as we find anything reasonable - we try to find what person two did, then three, then four, etc... we would probably find something pretty fast... But there is no way to prove that this is the only possible thing that happened. You still need to try all other combinations... one way or another.
That's why it really seems that CashFusion math checks out and it would be a pretty great way to anonymity in Bitcoin Cash.
Do you want to test it? See here.
Additional attack vector
Late addition: @ZeusOnPills gives an interesting attack vector on CashFusion in the comment below.
Let's imagine a a few CashFusions (or CashShuffles). So a user does a few Fusions, then closes the wallet.

Looks anonymous enough, very hard to guess who's who.
Then the user opens the wallet. Electron Cash, being a HD wallet, requests balances of all of your previous addresses, which makes the previous scheme kind of look like this:

The addresses in red are the addresses that Electron Cash just requested from the ElectrumX server that it just connected to. You can't see it on the blockchain, but if the ElectrumX server is logging this information - that could be really terrible, because not only you deanonymized yourself, but also severely reduced anonymity for other people...
One possible solution that I think can be done is to include additional addresses from each CashFusion in the future requests. This increases the load, but protects anonymity (somewhat). You should read the comments below - @ZeusOnPills has some interesting thoughts.


...and you will also help the author collect more tips.










Very interesting! What is the difference with CashShuffle?