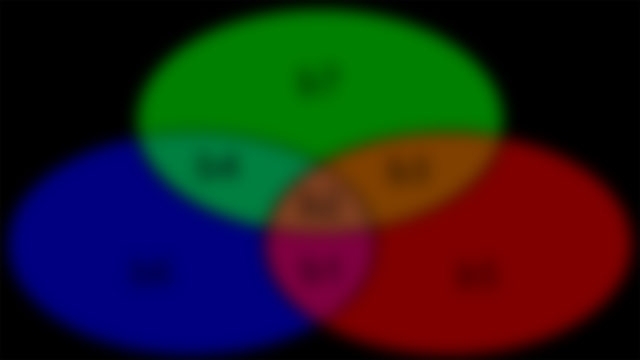
Figure 0. 7,4 Hamming Code Venn Diagram
0. Note
This is the fifth assignment from my Masters Applied Digital Information Theory Course which has never been published anywhere and I, as the author and copyright holder, license this assignment customized CC-BY-SA where anyone can share, copy, republish, and sell on condition to state my name as the author and notify that the original and open version available here.
1. Introduction
The previous 4th assignment demonstrate 1 bit error detection using 3,4 parity codes. On this assignment will be demonstrating 1 bit error correction using 7,4 hamming codes. On 3,4 parity codes we group 3 bits per block and perform exclusive or on each blocks to get a bit called the parity code bit and add it into the 4th bit of the blocks. A different approach for the 7,4 hamming codes we first group 4 bits per block, and then obtain the 3 hamming bit codes from the 4 bits for each blocks and add them which makes each blocks contained 7 bits. Suppose there are 4 bits as follows:
b1,b2,b3,b4
To get the hamming bit codes we do the following calculation:
b5=b1⊕b2⊕b3, b6=b1⊕b2⊕b4, b7=b1⊕b3⊕b4
Those bits will be added to the block:
b1,b2,b3,b4,b5,b6,b7
Following Table 1 are the complete list:
Table 1. Coding Table

On the receiver side the hamming codes is also constructed using the received first 4 bits of each blocks, then compare them with the hamming codes produced on the receiver side. Since the hamming codes were produced using the above equation (each codes uses different elements) we can know on which bit the error occurs, and a correction is performed. For example if receiver's b5, b6, b7 is different from transmitter's then an error on b1, if b5, b6 is different then an error occur on b2, if b5,b7 is different then an error occur on b3, if b6, b7 then b4, if b5 only then b5, if b6 only then b6, if b7 only then b7. Following Table 2 are the complete syndromes:
Table 2. Syndrome and Correction List

2. Memoryless Errors (Skew Tent Map)
On this simulation we will (1) generate a chaotic binary sequence from memoryless source (2) perform hamming coding (3) simulate through a noisy channel (4) perform error correction on receiver. We will calculate the practical probabilities of incorrect decoding and compare them theoretically defined by PI=1–PC where PC=7p(1-p)6 + (1-p)7 is the probability of correct decoding. The formula is derived from the probability of 1 bit error out of all possible error. Also we will compare the error probability of the binary sequence before correction and after correction. We will use critical point of c=0.499999 for generating the memoryless source, while we use c=1-p for generating the error sequence, and initial chaotic value for both is x(1)=0.333333 and various error probability p for the error sequence (noise). Generating the source will be the same as assignment 2, and generating the hamming codes is similar to 4th assignment except we input 3 extra bits in each blocks based on the initial 4 bits, which will make 7 bits. Like the previous assignment we perform exclusive or between the generated memoryless source and the error sequence to obtain the received sequence. On Table 3 is the simulation result of 1000000 (million) blocks (N) (7000000 bits) with error probability up to 0.4.
Table 3. simulation result of 1000000 (million) blocks (N) (7000000 bits) with error probability up to 0.4

3. Markov-type Errors (PWL Map)
Similar to section 2 but this time we generate the error sequence through Markov type or Piece Wise Linear (PWL) map. The theoretical incorrect error decoding is PI=1–PC and correct one:
PC = P(1)p2 (1-p)5 + 5P(0)p1 p2 (1-p1)4 + P(0)(1-p1)5 p1 + P(0)(1-p1)6
We use the same critical point and initial chaotic value. To generate the error sequence we use the PWL map with various p2 values and P1 = (1-c)/c P2, with c=1-p. On Table 4 is the theoretical result of 1000000 (million) blocks (N) (7000000 bits) with error probability up to 0.4, Table 5 is the simulation result, Table 6 is error probability before decoding, Table 7 is error probability after decoding.
Table 4. Theoretical Result

Table 5 Simulation Result

Table 6. Error Probability Before Decoding

Table 7. Error Probability After Decoding

4. Results
On Figure 1 shows that the error probability before and after decoding fluctuates on different error probability values (p) and type of sources (memoryless and p2s), but had one thing in common that belowp < 0.3 the error after decoding decreases, and unfortunately rises above that. The incorrect coding for memoryless is preferable when p < 0.1 but not recommended when above. For PWL with p2=0.1 shows low incorrect decoding amongst other p2. For other values there is a cutting point on p=0.2, below lower p2 shows lower incorrect decoding and viceversa.

Figure 1. Error vs Error Before and After Decoding

Figure 2. Error vs Incorrect Decoding
5. Source Code
The source code is written in Fortran95 which is said to be a good programming language for mathematics in the old days, the first one is for memoryless, and the first one is for PWL (markov).
program Memoryless_Error_Hamming
! For safe purposes
implicit none
! Type declarations
integer :: m, n1, n2, i, j, s1, s2, s3
real :: c, c_error, p, practical_error_before, p_practical_error_before, practical_error_after
real :: p_practical_error_after, incorrect_decoding, p_incorrect_decoding
real :: p_theory_correct_decoding, p_theory_incorrect_decoding
real, dimension(40000000) :: x
integer, dimension(40000000) :: bit
integer, dimension(70000000) :: bit_hamming, bit_error, bit_receiver, bit_hamming_uncorrected, bit_corrected
character(len=20) :: firstname, lastname, text
write (*,'(A)',advance='no') 'Enter number of blocks: '
read (*,*) m
n1 = m*4
n2 = m*7
c = 0.499999
! Memoryless Generated Source (here n is number of bits)
x(1) = 0.333333
do i = 1, n1-1
if (x(i) >= 0 .and. x(i) < c) then
x(i+1) = x(i)/c
bit(i) = 0
else
x(i+1) = (1-x(i))/(1-c)
bit(i) = 1
end if
end do
! Hamming Codes
j = 1
do i = 1, n2, 7
bit_hamming(i) = bit(j)
bit_hamming(i+1) = bit(j+1)
bit_hamming(i+2) = bit(j+2)
bit_hamming(i+3) = bit(j+3)
bit_hamming(i+4) = xor(xor(bit(j),bit(j+1)),bit(j+2))
bit_hamming(i+5) = xor(xor(bit(j),bit(j+1)),bit(j+3))
bit_hamming(i+6) = xor(xor(bit(j+1),bit(j+2)),bit(j+3))
j = j+4
end do
! Error Sequence
write (*,'(A)',advance='no') 'Enter error probability: '
read (*,*) p
c_error = 1 - p
do i = 1, n2
if (x(i) >= 0 .and. x(i) < c_error) then
x(i+1) = x(i)/c_error
bit_error(i) = 0
else
x(i+1) = (1-x(i))/(1-c_error)
bit_error(i) = 1
end if
end do
! Receiver Side (hamming encoded sequence + error sequence), calculate error probability before decoding, prefill future corrected bits
practical_error_before = 0;
do i = 1, n2
bit_receiver(i) = xor(bit_hamming(i), bit_error(i))
bit_corrected(i) = bit_receiver(i)
if (bit_receiver(i) /= bit_hamming(i)) then
practical_error_before = practical_error_before + 1
end if
end do
p_practical_error_before = practical_error_before/n2
! Perform Hamming coding again on the received bits
do i = 1, n2, 7
bit_hamming_uncorrected(i) = bit_receiver(i)
bit_hamming_uncorrected(i+1) = bit_receiver(i+1)
bit_hamming_uncorrected(i+2) = bit_receiver(i+2)
bit_hamming_uncorrected(i+3) = bit_receiver(i+3)
bit_hamming_uncorrected(i+4) = xor(xor(bit_receiver(i),bit_receiver(i+1)),bit_receiver(i+2))
bit_hamming_uncorrected(i+5) = xor(xor(bit_receiver(i),bit_receiver(i+1)),bit_receiver(i+3))
bit_hamming_uncorrected(i+6) = xor(xor(bit_receiver(i+1),bit_receiver(i+2)),bit_receiver(i+3))
end do
! Error Correction based on symptoms, "&" is placed to continue next line (fortran95 cannot read long lines)
do i = 1, n2, 7
if ((bit_hamming_uncorrected(i+4) /= bit_receiver(i+4)) .and. (bit_hamming_uncorrected(i+5) /= bit_receiver(i+5)) &
.and. (bit_hamming_uncorrected(i+6) /= bit_receiver(i+6))) then
bit_corrected(i) = xor(bit_receiver(i),1)
else if ((bit_hamming_uncorrected(i+4) /= bit_receiver(i+4)) .and. (bit_hamming_uncorrected(i+5) /= bit_receiver(i+5)) &
.and. (bit_hamming_uncorrected(i+6) == bit_receiver(i+6))) then
bit_corrected(i+1) = xor(bit_receiver(i+1),1)
else if ((bit_hamming_uncorrected(i+4) /= bit_receiver(i+4)) .and. (bit_hamming_uncorrected(i+5) == bit_receiver(i+5)) &
.and. (bit_hamming_uncorrected(i+6) /= bit_receiver(i+6))) then
bit_corrected(i+2) = xor(bit_receiver(i+2),1)
else if ((bit_hamming_uncorrected(i+4) == bit_receiver(i+4)) .and. (bit_hamming_uncorrected(i+5) /= bit_receiver(i+5)) &
.and. (bit_hamming_uncorrected(i+6) /= bit_receiver(i+6))) then
bit_corrected(i+3) = xor(bit_receiver(i+3),1)
else if ((bit_hamming_uncorrected(i+4) /= bit_receiver(i+4)) .and. (bit_hamming_uncorrected(i+5) == bit_receiver(i+5)) &
.and. (bit_hamming_uncorrected(i+6) == bit_receiver(i+6))) then
bit_corrected(i+4) = xor(bit_receiver(i+4),1)
else if ((bit_hamming_uncorrected(i+4) == bit_receiver(i+4)) .and. (bit_hamming_uncorrected(i+5) /= bit_receiver(i+5)) &
.and. (bit_hamming_uncorrected(i+6) == bit_receiver(i+6))) then
bit_corrected(i+5) = xor(bit_receiver(i+5),1)
else if ((bit_hamming_uncorrected(i+4) == bit_receiver(i+4)) .and. (bit_hamming_uncorrected(i+5) == bit_receiver(i+5)) &
.and. (bit_hamming_uncorrected(i+6) /= bit_receiver(i+6))) then
bit_corrected(i+6) = xor(bit_receiver(i+6),1)
end if
end do
! Error Probability After Decoding
practical_error_after = 0;
do i = 1, n2
if (bit_corrected(i) /= bit_hamming(i)) then
practical_error_after = practical_error_after + 1
end if
end do
p_practical_error_after = practical_error_after/n2
! Probability of Correct, and incorrect decoding
p_theory_correct_decoding = (7*p*(1-p)*(1-p)*(1-p)*(1-p)*(1-p)*(1-p))+((1-p)*(1-p)*(1-p)*(1-p)*(1-p)*(1-p)*(1-p))
p_theory_incorrect_decoding = 1 - p_theory_correct_decoding
incorrect_decoding = 0
do i = 1, n2, 7
if ((bit_corrected(i) /= bit_hamming(i)) .or. (bit_corrected(i+1) /= bit_hamming(i+1)) .or. &
(bit_corrected(i+2) /= bit_hamming(i+2)) .or. (bit_corrected(i+3) /= bit_hamming(i+3)) .or. &
(bit_corrected(i+4) /= bit_hamming(i+4)) .or. (bit_corrected(i+5) /= bit_hamming(i+5)) .or. &
(bit_corrected(i+6) /= bit_hamming(i+6))) then
incorrect_decoding = incorrect_decoding + 1
end if
end do
p_incorrect_decoding = incorrect_decoding/m
! Results
write (*,'(A)',advance='no') 'Practical error before decoding: '
write (*,*) practical_error_before
write (*,'(A)',advance='no') 'Practical error after decoding: '
write (*,*) practical_error_after
write (*,'(A)',advance='no') 'Probability practical error before decoding: '
write (*,*) p_practical_error_before
write (*,'(A)',advance='no') 'Probability practical error after decoding: '
write (*,*) p_practical_error_after
write (*,'(A)',advance='no') 'Incorrect decoding: '
write (*,*) incorrect_decoding
write (*,'(A)',advance='no') 'Probability of incorrect decoding: '
write (*,*) p_incorrect_decoding
write (*,'(A)',advance='no') 'Theoretical probability of incorrect decoding: '
write (*,*) p_theory_incorrect_decoding
! Debugging purposes, uncomment them to see binary sequences, max 18 blocks
! do i = 1, n2
! write(*,'(1i1.1)',advance='no') bit_hamming(i)
! end do
! write (*,*) ' '
! do i = 1, n2
! write(*,'(1i1.1)',advance='no') bit_error(i)
! end do
! write (*,*) ' '
! do i = 1, n2
! write(*,'(1i1.1)',advance='no') bit_receiver(i)
! end do
! write (*,*) ' '
! do i = 1, n2
! write(*,'(1i1.1)',advance='no') bit_corrected(i)
! end do
! write (*,*) ' '
end program Memoryless_Error_Hammingprogram Piece_Wise_Linear_Error
! For safe purposes
implicit none
! Type declarations
integer :: m, n1, n2, i, j, s1, s2, s3
real :: c, c_error, p, practical_error_before, p_practical_error_before, practical_error_after
real :: p_practical_error_after, incorrect_decoding, p_incorrect_decoding
real :: p_theory_correct_decoding, p_theory_incorrect_decoding
real :: p1, p2, a, a1, a2, a3, c1, c2, d1, d2
real, dimension(40000000) :: x
integer, dimension(40000000) :: bit
integer, dimension(70000000) :: bit_hamming, bit_error, bit_receiver, bit_hamming_uncorrected, bit_corrected
character(len=20) :: firstname, lastname, text
write (*,'(A)',advance='no') 'Enter number of blocks: '
read (*,*) m
n1 = m*4
n2 = m*7
c = 0.499999
x(1) = 0.333333
! Uncomment to use memoryless source
! Memoryless Generated Source (here n is number of bits)
! x(1) = 0.333333
! do i = 1, n1-1
! if (x(i) >= 0 .and. x(i) < c) then
! x(i+1) = x(i)/c
! bit(i) = 0
! else
! x(i+1) = (1-x(i))/(1-c)
! bit(i) = 1
! end if
! end do
! PWL Generated Source
p1 = (1-c)*p2/c
a = 1/(1-(p1+p2))
if (p1+p2 < 1) then
c1 = c-(c/a)
c2 = c+((1-c)/a)
d1 = c1*(1-c)
d2 = 1-((1-c2)*c)
a1 = -c/(c1-d1)
a2 = a
a3 = (c-1)/(d2-c2)
do i = 1, n2
if (x(i) >= 0 .and. x(i) < c1) then
x(i+1) = (a1*(x(i)-d1))+c
else if (x(i) >= c1 .and. x(i) < c2) then
x(i+1) = a2*(x(i)-c1)
else
x(i+1) = (a3*(x(i)-c2))+1
end if
if (x(i) >= 0 .and. x(i) < c) then
bit(i) = 0
else
bit(i) = 1
end if
end do
else
c1 = c-((c-1)/a)
c2 = c-(c/a)
d1 = c1*(1-c)
d2 = 1-((1-c2)*(1-c))
a1 = -c/(c1-d1)
a2 = a
a3 = c/(d2-c2)
do i = 1, n2
if (x(i) >= 0 .and. x(i) < c1) then
x(i+1) = (a1*(x(i)-d1))+c
else if (x(i) >= c1 .and. x(i) < c2) then
x(i+1) = (a2*(x(i)-c1))+1
else
x(i+1) = a3*(x(i)-c2)
end if
if (x(i) >= 0 .and. x(i) < c) then
bit(i) = 0
else
bit(i) = 1
end if
end do
end if
! Hamming Codes
j = 1
do i = 1, n2, 7
bit_hamming(i) = bit(j)
bit_hamming(i+1) = bit(j+1)
bit_hamming(i+2) = bit(j+2)
bit_hamming(i+3) = bit(j+3)
bit_hamming(i+4) = xor(xor(bit(j),bit(j+1)),bit(j+2))
bit_hamming(i+5) = xor(xor(bit(j),bit(j+1)),bit(j+3))
bit_hamming(i+6) = xor(xor(bit(j+1),bit(j+2)),bit(j+3))
j = j+4
end do
! Error Sequence
write (*,'(A)',advance='no') 'Enter error probability: '
read (*,*) p
c_error = 1 - p
write (*,'(A)',advance='no') 'Enter p2: '
read (*,*) p2
p1 = (1-c_error)*p2/c_error
a = 1/(1-(p1+p2))
if (p1+p2 < 1) then
c1 = c_error-(c_error/a)
c2 = c_error+((1-c_error)/a)
d1 = c1*(1-c_error)
d2 = 1-((1-c2)*c_error)
a1 = -c_error/(c1-d1)
a2 = a
a3 = (c_error-1)/(d2-c2)
do i = 1, n2
if (x(i) >= 0 .and. x(i) < c1) then
x(i+1) = (a1*(x(i)-d1))+c_error
else if (x(i) >= c1 .and. x(i) < c2) then
x(i+1) = a2*(x(i)-c1)
else
x(i+1) = (a3*(x(i)-c2))+1
end if
if (x(i) >= 0 .and. x(i) < c_error) then
bit_error(i) = 0
else
bit_error(i) = 1
end if
end do
else
c1 = c_error-((c_error-1)/a)
c2 = c_error-(c_error/a)
d1 = c1*(1-c_error)
d2 = 1-((1-c2)*(1-c_error))
a1 = -c_error/(c1-d1)
a2 = a
a3 = c_error/(d2-c2)
do i = 1, n2
if (x(i) >= 0 .and. x(i) < c1) then
x(i+1) = (a1*(x(i)-d1))+c_error
else if (x(i) >= c1 .and. x(i) < c2) then
x(i+1) = (a2*(x(i)-c1))+1
else
x(i+1) = a3*(x(i)-c2)
end if
if (x(i) >= 0 .and. x(i) < c_error) then
bit_error(i) = 0
else
bit_error(i) = 1
end if
end do
end if
! Receiver Side (hamming encoded sequence + error sequence), calculate error probability before decoding, prefill future corrected bits
practical_error_before = 0;
do i = 1, n2
bit_receiver(i) = xor(bit_hamming(i), bit_error(i))
bit_corrected(i) = bit_receiver(i)
if (bit_receiver(i) /= bit_hamming(i)) then
practical_error_before = practical_error_before + 1
end if
end do
p_practical_error_before = practical_error_before/n2
! Perform Hamming coding again on the received bits
do i = 1, n2, 7
bit_hamming_uncorrected(i) = bit_receiver(i)
bit_hamming_uncorrected(i+1) = bit_receiver(i+1)
bit_hamming_uncorrected(i+2) = bit_receiver(i+2)
bit_hamming_uncorrected(i+3) = bit_receiver(i+3)
bit_hamming_uncorrected(i+4) = xor(xor(bit_receiver(i),bit_receiver(i+1)),bit_receiver(i+2))
bit_hamming_uncorrected(i+5) = xor(xor(bit_receiver(i),bit_receiver(i+1)),bit_receiver(i+3))
bit_hamming_uncorrected(i+6) = xor(xor(bit_receiver(i+1),bit_receiver(i+2)),bit_receiver(i+3))
end do
! Error Correction based on symptoms, "&" is placed to continue next line (fortran95 cannot read long lines)
do i = 1, n2, 7
if ((bit_hamming_uncorrected(i+4) /= bit_receiver(i+4)) .and. (bit_hamming_uncorrected(i+5) /= bit_receiver(i+5)) &
.and. (bit_hamming_uncorrected(i+6) /= bit_receiver(i+6))) then
bit_corrected(i) = xor(bit_receiver(i),1)
else if ((bit_hamming_uncorrected(i+4) /= bit_receiver(i+4)) .and. (bit_hamming_uncorrected(i+5) /= bit_receiver(i+5)) &
.and. (bit_hamming_uncorrected(i+6) == bit_receiver(i+6))) then
bit_corrected(i+1) = xor(bit_receiver(i+1),1)
else if ((bit_hamming_uncorrected(i+4) /= bit_receiver(i+4)) .and. (bit_hamming_uncorrected(i+5) == bit_receiver(i+5)) &
.and. (bit_hamming_uncorrected(i+6) /= bit_receiver(i+6))) then
bit_corrected(i+2) = xor(bit_receiver(i+2),1)
else if ((bit_hamming_uncorrected(i+4) == bit_receiver(i+4)) .and. (bit_hamming_uncorrected(i+5) /= bit_receiver(i+5)) &
.and. (bit_hamming_uncorrected(i+6) /= bit_receiver(i+6))) then
bit_corrected(i+3) = xor(bit_receiver(i+3),1)
else if ((bit_hamming_uncorrected(i+4) /= bit_receiver(i+4)) .and. (bit_hamming_uncorrected(i+5) == bit_receiver(i+5)) &
.and. (bit_hamming_uncorrected(i+6) == bit_receiver(i+6))) then
bit_corrected(i+4) = xor(bit_receiver(i+4),1)
else if ((bit_hamming_uncorrected(i+4) == bit_receiver(i+4)) .and. (bit_hamming_uncorrected(i+5) /= bit_receiver(i+5)) &
.and. (bit_hamming_uncorrected(i+6) == bit_receiver(i+6))) then
bit_corrected(i+5) = xor(bit_receiver(i+5),1)
else if ((bit_hamming_uncorrected(i+4) == bit_receiver(i+4)) .and. (bit_hamming_uncorrected(i+5) == bit_receiver(i+5)) &
.and. (bit_hamming_uncorrected(i+6) /= bit_receiver(i+6))) then
bit_corrected(i+6) = xor(bit_receiver(i+6),1)
end if
end do
! Error Probability After Decoding
practical_error_after = 0;
do i = 1, n2
if (bit_corrected(i) /= bit_hamming(i)) then
practical_error_after = practical_error_after + 1
end if
end do
p_practical_error_after = practical_error_after/n2
! Probability of Correct, and incorrect decoding
p_theory_correct_decoding = (((1-c_error)*p2*((1-p1)**5)) + (5*c_error*p1*p2*((1-p1)**4)) + (c_error*((1-p1)**5)*p1) + &
(c_error*((1-p1)**6)))
p_theory_incorrect_decoding = 1 - p_theory_correct_decoding
incorrect_decoding = 0
do i = 1, n2, 7
if ((bit_corrected(i) /= bit_hamming(i)) .or. (bit_corrected(i+1) /= bit_hamming(i+1)) .or. &
(bit_corrected(i+2) /= bit_hamming(i+2)) .or. (bit_corrected(i+3) /= bit_hamming(i+3)) .or. &
(bit_corrected(i+4) /= bit_hamming(i+4)) .or. (bit_corrected(i+5) /= bit_hamming(i+5)) .or. &
(bit_corrected(i+6) /= bit_hamming(i+6))) then
incorrect_decoding = incorrect_decoding + 1
end if
end do
p_incorrect_decoding = incorrect_decoding/m
! Results
write (*,'(A)',advance='no') 'Practical error before decoding: '
write (*,*) practical_error_before
write (*,'(A)',advance='no') 'Practical error after decoding: '
write (*,*) practical_error_after
write (*,'(A)',advance='no') 'Probability practical error before decoding: '
write (*,*) p_practical_error_before
write (*,'(A)',advance='no') 'Probability practical error after decoding: '
write (*,*) p_practical_error_after
write (*,'(A)',advance='no') 'Incorrect decoding: '
write (*,*) incorrect_decoding
write (*,'(A)',advance='no') 'Probability of incorrect decoding: '
write (*,*) p_incorrect_decoding
write (*,'(A)',advance='no') 'Theoretical probability of incorrect decoding: '
write (*,*) p_theory_incorrect_decoding
! Debugging purposes, uncomment them to see binary sequences, max 18 blocks
! do i = 1, n2
! write(*,'(1i1.1)',advance='no') bit_hamming(i)
! end do
! write (*,*) ' '
! do i = 1, n2
! write(*,'(1i1.1)',advance='no') bit_error(i)
! end do
! write (*,*) ' '
! do i = 1, n2
! write(*,'(1i1.1)',advance='no') bit_receiver(i)
! end do
! write (*,*) ' '
! do i = 1, n2
! write(*,'(1i1.1)',advance='no') bit_corrected(i)
! end do
! write (*,*) ' '
end program Piece_Wise_Linear_ErrorMirrors
https://www.publish0x.com/fajar-purnama-academics/74-hamming-codes-xervrkp?a=4oeEw0Yb0B&tid=readcash
https://0darkking0.blogspot.com/2021/01/74-hamming-codes.html
https://0fajarpurnama0.medium.com/7-4-hamming-codes-218a9c933786
https://0fajarpurnama0.github.io/masters/2020/09/15/hamming-codes
https://hicc.cs.kumamoto-u.ac.jp/~fajar/masters/hamming-codes
https://steemit.com/math/@fajar.purnama/7-4-hamming-codes?r=fajar.purnama
https://stemgeeks.net/math/@fajar.purnama/7-4-hamming-codes?ref=fajar.purnama
https://blurtter.com/blurtech/@fajar.purnama/7-4-hamming-codes?referral=fajar.purnama
https://0fajarpurnama0.wixsite.com/0fajarpurnama0/post/7-4-hamming-codes
https://0fajarpurnama0.cloudaccess.host/index.php/9-fajar-purnama-academics/190-7-4-hamming-codes
https://www.uptrennd.com/post-detail/7-4-hamming-codes~ODU1MjQy

...and you will also help the author collect more tips.