0. Note
This is the fourth assignment from my Masters Applied Digital Information Theory Course which has never been published anywhere and I, as the author and copyright holder, license this assignment customized CC-BY-SA where anyone can share, copy, republish, and sell on condition to state my name as the author and notify that the original and open version available here.
1. Introduction
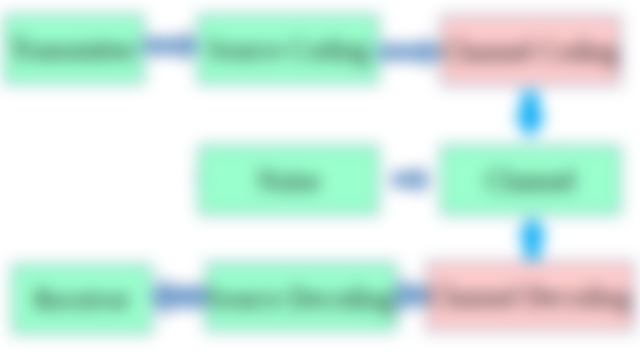
On Figure 1 of Shannon Communication Model, the previous assignments on memoryless and Markov's source is on the first block transmitter (source), while this fourth assignment is on the channel coding and decoding. It will be demonstrated a binary source coded with parity check codes , going through a noisy channel with the specified bit error rate, and decoded on with parity check. On the receiver side will compare the theoretical and practical error using parity check.

Figure 1. Shannon Communication Model
A parity (3,4) check coding takes 3 bits + 1 into 1 block with the last bit as the parity bit obtained by performing exclusive or (xor) on the 3 bits. The blocks are then transmitted and xor is again performed on the decoder side on the 4 bits of the block, and if the result is 0 then it's not regarded as error, but if the result is 1 then it's regarded as error. Looking this checking method it can detect errors when odd numbers of bits error occurs, but it cannot detect when even number of error occurs. This can be demonstrated on the following table.
Table 1. Parity Check Examples

2. Skew Tent Map
The binary sequence on the transmitter is generated by means of 2nd assignment of skew tent map with initial x[1] = 0.1 and c = 0.499999. This time we generated in a million blocks with each blocks contains 3 + 1 bits. On the source we generated the initial bits of normal means on assignment 2, but then we slip a parity bit on every 4th increments of the sequence (on the actual code we made 2 sequence where the first sequence as a reference for the sequence with parity bit, b2[0] = b1[0], b2[1] = b1[1], b2[2] = b1[2], b2[3] = b1[0]⊕b1[1]⊕b1[2], b2[4] = b1[3], b2[5] = b1[4], b2[6] = b1[5], b2[7] = b1[3]⊕b1[4]⊕b1[5], and so on).
After that we simulate an error sequence with initial x_err[0] = 0.500001, error probability p varies, and c_err = 1-p. Then as per section 1 we xor the parity coded binary sequence with the error simulated generated sequence, obtaining the binary sequence at the receiver. We can find the total errors by comparing the binary sequence on the transmitter side (before xor by error sequence) and on the receiver side (after xor by error sequence). Then we perform xor on each blocks (every 4 bits) of the receiver binary sequence to get the detected error. Finally we calculate the difference between total errors (real) and detected error to find the practical undetected error. The theoretical undetected error can be calculated using the following equation: Pu = 6p2(1-p)2+p4 which is actually a formula of the probability of even blocks after passing through noisy channel with defined error probability.
Table 2. Trials of Error Probability to Undetected Error

3. PWL Map
Roughly similar to 2nd section but this time use PWL Map error sequence. We start by choosing p2, but generating the error sequence we defined c_err as 1-p (initial c remain 0.499999 and p1 is computed), with p2 still the same, but p1_err is defined based on c_err. Automatically slop a changes and the sequence was generated. The process is the same after that, with the theoretical of undetected error as Pu = P(0)((1-p1)p1(1-p2)+p1(1-p2)p2+p1p2p1) + p(1)(p2(1-p1)p1+p2p1p2+(1-p2)p2(1-p1)+(1-p2)(1-p2)(1-p2)), again is actually a formula of even blocks probability after passing through noisy channel with defined error probability.
Table 3. Probability of Practical Undetected Error of different values of p to values of p2

Table 4. Probability of Theoretical Undetected Error of different values of p to values of p2

4. Summary
From above the practical value almost matches the theoretical value. As on Figure 2 plotted based on tables above, for error probability below 0.2 the skew tent map has lower undetected error probability which good to use on channels with little noise. For above it's better to use PWL but with p2 value lower than 0.5.

Figure 2. Probability Error vs Undetected Error Probability
5. Source Code
The source code is divided into 2 one for skew tent map and the other for PWL map written in C++.
//============================================================================
// Name : skew-tent-map.cpp
// Author : Fajar Purnama 152-D8713
// Version : 0.9
// Copyright : Free to distributed with credits to the author.
// Description : Source Code for Skew Tent Map in C++
//============================================================================
#include <iostream>
using namespace std;
int main() {
cout << "!!!Hello World!!!" << endl; // prints !!!Hello World!!!
int N = 10000*3, bin[N]; float x[N], c = 0.499999; x[0] = 0.3;
// N = number of bits (1 block = 3 bits), c = critical point, x[0] = initial value, x[N] = chaotic sequence, and bin[N] = binary sequence
// From here is 2nd Assignment
for (int i = 0; i < N; ++i){
if (x[i] >= 0 && x[i] < c) {
x[i+1] = x[i]/c;
bin[i] = 0;
} else {
x[i+1] = (1-x[i])/(1-c);
bin[i] = 1;
}
}
// Insert bit parity on every 4th bit
int j = 0, bin_par[N+(N/3)];
for (int i = 0; i < N+(N/3); i += 4){
bin_par[i] = bin[j];
bin_par[i+1] = bin[j+1];
bin_par[i+2] = bin[j+2];
bin_par[i+3] = bin_par[i]^bin_par[i+1]^bin_par[i+2];
j += 3;
}
// Generate error sequence
int bin_err[N+(N/3)]; float p;
cout << "Enter error probability: "; cin >> p;
float c_err = 1-p, x_err[N+(N/3)]; x_err[0]=0.500001;
for (int i = 0; i < N+(N/3); ++i){
if (x_err[i] >= 0 && x_err[i] < c_err) {
x_err[i+1] = x_err[i]/c_err;
bin_err[i] = 0;
} else {
x_err[i+1] = (1-x_err[i])/(1-c_err);
bin_err[i] = 1;
}
}
// Generate receiver side = parity sequence XOR error sequence
int bin_r[N+(N/3)];
for (int i = 0; i < N+(N/3); ++i){
bin_r[i] = bin_par[i] ^ bin_err[i];
}
for (int i = 0; i < N+(N/3); ++i){
cout << bin_err[i];
}
cout << endl;
for (int i = 0; i < N+(N/3); ++i){
cout << bin_par[i];
}
cout << endl;
for (int i = 0; i < N+(N/3); ++i){
cout << bin_r[i];
}
cout << endl << endl;
// total error, detected error, undetected error
float total_error = 0, detected_error = 0, undetected_error = 0;
float p_theory = ((6*p*p)*((1-p)*(1-p))+(p*p*p*p));
for (int i = 0; i < N+(N/3); i += 4){
if((bin_par[i] != bin_r[i])||(bin_par[i+1] != bin_r[i+1])||(bin_par[i+2] != bin_r[i+2])||(bin_par[i+3] != bin_r[i+3])){
++total_error;
}
if((bin_r[i]^bin_r[i+1]^bin_r[i+2]^bin_r[i+3])==1){
++detected_error;
}
}
undetected_error = total_error - detected_error;
float p_total_error = total_error/(N/3);
float p_detected_error = detected_error/(N/3);
float p_undetected_error = undetected_error/(N/3);
cout << "total error = " << total_error << endl;
cout << "detected error = " << detected_error << endl;
cout << endl;
cout << "undetected error = " << undetected_error << endl;
cout << "probability of total error = " << p_total_error << endl;
cout << "probability of detected error = " << p_detected_error << endl;
cout << "probability of undetected error = " << p_undetected_error << endl;
cout << "theory = " << p_theory << endl;
return 0;
}//============================================================================
// Name : 43-single-parity-check-codes-large.cpp
// Author : Fajar Purnama 152-D8713
// Version : 0.9
// Copyright : Free to distributed with credits to the author.
// Description : Source Code for PWL Tent Map in C++
//============================================================================
#include <iostream>
using namespace std;
int main() {
int n;
cout << "Enter number of blocks: "; cin >> n;
int N = n*3; float p1, p2, c, c1, c2, d1, d2, a, a1, a2, a3;
c = 0.499999; cout << "Enter value of p2: "; cin >> p2;
p1 = (1-c)*p2/c;
a = 1/(1-(p1+p2));
int* bin = new int[N]; // need to do this because int main cannot hold large numbers, a stack overflow occurs so need to allocate to new heap
float* x = new float[N]; x[0] = 0.1;
// N = number of bits (1 block = 3 bits), c = critical point, x[0] = initial value, x[N] = chaotic sequence, and bin[N] = binary sequence
// From here is 3rd Assignment
if (p1+p2 < 1){
c1 = c-(c/a);
c2 = c+((1-c)/a );
d1 = c1*(1-c);
d2 = 1-((1-c2)*c);
a1 = -c/(c1-d1);
a2 = a;
a3 = (c-1)/(d2-c2);
for (int i = 0; i < N; ++i){
if (x[i] >= 0 && x[i] < c1) {
x[i+1] = (a1*(x[i]-d1))+c;
} else if(x[i] >= c1 && x[i] < c2) {
x[i+1] = a2*(x[i]-c1);
} else {
x[i+1] = (a3*(x[i]-c2))+1;
}
if (x[i] < c){
bin[i] = 0;
} else {
bin[i] = 1;
}
}
} else if (p1+p2 > 1){
c1 = c-((c-1)/a);
c2 = c-(c/a);
d1 = c1*(1-c);
d2 = 1-((1-c2)*(1-c));
a1 = -c/(c1-d1);
a2 = a;
a3 = c/(d2-c2);
for (int i = 0; i < N; ++i){
if (x[i] >= 0 && x[i] < c1) {
x[i+1] = (a1*(x[i]-d1))+c;
} else if(x[i] >= c1 && x[i] < c2) {
x[i+1] = (a2*(x[i]-c1))+1;
} else {
x[i+1] = a3*(x[i]-c2);
}
if (x[i] < c){
bin[i] = 0;
} else {
bin[i] = 1;
}
}
} else {
cout << "you can't do this" << endl;
}
// Insert bit parity on every 4th bit
int j = 0; int* bin_par = new int[N+(N/3)];
for (int i = 0; i < N+(N/3); i += 4){
bin_par[i] = bin[j];
bin_par[i+1] = bin[j+1];
bin_par[i+2] = bin[j+2];
bin_par[i+3] = bin_par[i]^bin_par[i+1]^bin_par[i+2];
j += 3;
}
// Generate error sequence
int* bin_err = new int[N+(N/3)]; float p, p1_err;
float* x_err = new float[N+(N/3)]; x_err[0]=x[0];
cout << "Enter error probability :"; cin >> p;
float c_err = 1-p;
p1_err = (1-c_err)*p2/c_err;
a = 1/(1-(p1_err+p2));
if (p1_err+p2 < 1){
c1 = c_err-(c_err/a);
c2 = c_err+((1-c_err)/a );
d1 = c1*(1-c_err);
d2 = 1-((1-c2)*c_err);
a1 = -c_err/(c1-d1);
a2 = a;
a3 = (c_err-1)/(d2-c2);
for (int i = 0; i < N+(N/3); ++i){
if (x_err[i] >= 0 && x_err[i] < c1) {
x_err[i+1] = (a1*(x_err[i]-d1))+c_err;
} else if(x_err[i] >= c1 && x_err[i] < c2) {
x_err[i+1] = a2*(x_err[i]-c1);
} else {
x_err[i+1] = (a3*(x_err[i]-c2))+1;
}
if (x_err[i] < c_err){
bin_err[i] = 0;
} else {
bin_err[i] = 1;
}
}
} else if (p1_err+p2 > 1){
c1 = c_err-((c_err-1)/a);
c2 = c_err-(c_err/a);
d1 = c1*(1-c_err);
d2 = 1-((1-c2)*(1-c_err));
a1 = -c_err/(c1-d1);
a2 = a;
a3 = c_err/(d2-c2);
for (int i = 0; i < N+(N/3); ++i){
if (x_err[i] >= 0 && x_err[i] < c1) {
x_err[i+1] = (a1*(x_err[i]-d1))+c_err;
} else if(x_err[i] >= c1 && x_err[i] < c2) {
x_err[i+1] = (a2*(x_err[i]-c1))+1;
} else {
x_err[i+1] = a3*(x_err[i]-c2);
}
if (x_err[i] < c_err){
bin_err[i] = 0;
} else {
bin_err[i] = 1;
}
}
} else {
cout << "you can't do this" << endl;
}
// Generate receiver side = parity sequence XOR error sequence
int* bin_r = new int[N+(N/3)];
for (int i = 0; i < N+(N/3); ++i){
bin_r[i] = bin_par[i] ^ bin_err[i];
}
/* Debugging Purpose
for (int i = 0; i < N+(N/3); ++i){
cout << bin_err[i];
}
cout << endl;
for (int i = 0; i < N+(N/3); ++i){
cout << bin_par[i];
}
cout << endl;
for (int i = 0; i < N+(N/3); ++i){
cout << bin_r[i];
}
cout << endl << endl; */
// total error, detected error, undetected error
float total_error = 0, detected_error = 0, undetected_error = 0;
float p_theory = (c_err*(((1-p1_err)*p1_err*(1-p2))+(p1_err*(1-p2)*p2)+(p1_err*p2*p1_err)))+((1-c_err)*((p2*(1-p1_err)*p1_err)+(p2*p1_err*p2)+((1-p2)*p2*(1-p1_err))+((1-p2)*(1-p2)*(1-p2))));
//float p_theory = (c*(((1-p1)*p1*(1-p2))+(p1*(1-p2)*p2)+(p1*p2*p1)))+((1-c)*((p2*(1-p1)*p1)+(p2*p1*p2)+((1-p2)*p2*(1-p1))+((1-p2)*(1-p2)*(1-p2))));
for (int i = 0; i < N+(N/3); i += 4){
if((bin_par[i] != bin_r[i])||(bin_par[i+1] != bin_r[i+1])||(bin_par[i+2] != bin_r[i+2])||(bin_par[i+3] != bin_r[i+3])){
++total_error;
}
if((bin_r[i]^bin_r[i+1]^bin_r[i+2]^bin_r[i+3])==1){
++detected_error;
}
}
undetected_error = total_error - detected_error;
float p_total_error = total_error/(N/3);
float p_detected_error = detected_error/(N/3);
float p_undetected_error = undetected_error/(N/3);
cout << "total error = " << total_error << endl;
cout << "detected error = " << detected_error << endl;
cout << endl;
cout << "undetected error = " << undetected_error << endl;
cout << "probability of total error = " << p_total_error << endl;
cout << "probability of detected error = " << p_detected_error << endl;
cout << "probability of undetected error = " << p_undetected_error << endl;
cout << "theory = " << p_theory << endl;
return 0;
}Mirrors

...and you will also help the author collect more tips.