The theory of relativity is one of the most important discoveries in modern physics. It was developed by Albert Einstein and has been pivotal to our understanding of the universe. But what exactly does it stand for? Let me break down some key points, like the equivalence principle, length contraction, time dilation, and more!
The Equivalence Principle: Defined
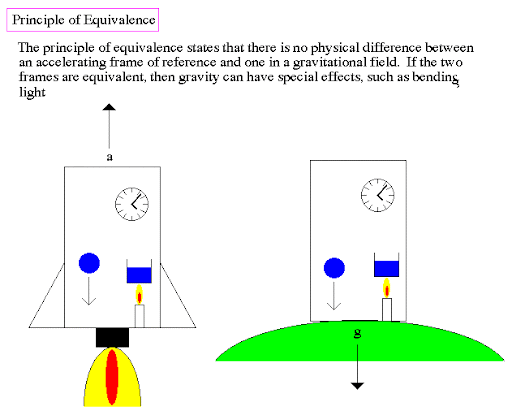
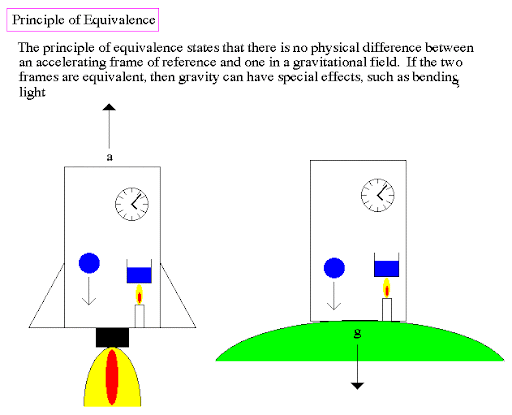
According to the equivalence principle, gravity is the same as inertial motion. Or in other words, an object will fall at the same speed on a moving train as it would if it were dropped from the train in a vacuum. This concept was published by Einstein in 1907.
This brings us to one of two major points of relativity- The idea that velocity and mass are not linked. In Newtonian physics (the previous understanding), there was absolutely no connection between velocity and mass. Objects with greater mass necessarily moved slower than objects with lower mass under similar forces, whether those forces were gravitational or otherwise.

A bowling ball has more mass than a baseball, so it needs to be hit faster to go the same distance. This is true in Newtonian physics, but not in relativity- It does not matter how fast or slow an object moves, as long as it keeps its momentum.
In sum, this principle states that gravity and inertia are essentially the same thing: One cannot be distinguished from the other. The equivalence principle has been confirmed by countless experiments over the last century. But some argue that there is one experiment which disproves it…
Related Post: Why Should You, or Anyone Else Who Cares About Space Travel Should to Learn Physics?
Physical Confirmation of the Equivalence Principle
There are actually many different tests for whether something "falls" at a different rate than something else- You can use clocks on board falling airplanes or satellites to time how long they take to fall towards earth (The International Space Station falls faster than earth).
In the 1970s, physicists performed an experiment in which they fired photons (packets of energy) at a beam splitter-a device with two small mirrors that let light through. They placed a detector on one side, and another on the other. The idea was if gravity affects everything equally, then the beams should hit both detectors at exactly the same time.
But what they observed shocked everyone: The beam that had been twice reflected took four times longer than the beam that had only gone once to reach its destination! This is because gravitational field strength doubles for every additional distance you drop through it.

This test disproves Einstein's equivalence principle as far as people like Sir Isaac Newton are concerned. But not according to Einstein himself.
He was actually tested with the same beam splitter experiment and agreed that the results were weird. But he knew what was going on (why the effect happened) from years of earlier research into his theory of relativity; All objects fall at a constant speed in a vacuum. So when gravity is doubled by reflection, everything still falls at its own independent rate!
It wasn't until later experiments with quantum foam in 1994 that Einstein's general theory was proven true according to everyone…
Length Contraction: What it Means

If you're standing next to an object and looking down on it, it appears as if each side is longer than if you looked straight across. If we take two rulers- one normal ruler and another ruler which has had every other section cut out- we can measure this effect. And come to find out, the removed sections are infinitely long!
Related Post: Why Should You, or Anyone Else Who Cares About Space Travel Should to Learn Physics?
How can that be? This is because of length contraction, a key tenet of Einstein's theory of relativity. The answer lies in understanding what it means…
In relativity, all objects get shorter when they move near the speed of light. When you hold a ruler and walk through an airport in superman fashion (with arms extended), you'll notice your ruler gets smaller as time passes by; Distance between the marks on it isn't constant anymore! Subatomic particles also appear to shrink in size as they near the speed of light; In reality, though, their space contracts together so that only one dimension remains while disappear from reality. Despite the apparent mind-numbing nature of this statement, it makes sense if you understand special relativity in detail…
This is because a) it only happens to objects which are moving at or near the speed of light and b) these particles can still be measured by their size; They're just more difficult to see (this effect does not occur with slower masses like electrons). According to the length contraction formula , this size shrinkage happens as follows: L = L0 [1 - v2/c2 ]
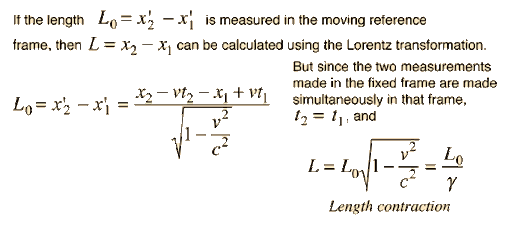
Where L is how long an object appears to be, and L 0 is how long it actually is. The constant c represents the speed of light in a vacuum- 300 million meters per second! And because L is measured in meters and v is measured in m/s, we get the following graph:

Although nothing can move faster than the speed of light (that's just physical law), this formula can be used to determine how an object would appear if it did. For example: Let's say you had a radar on an airplane which detected a UFO as it passed by at 97% of the speed of light. According to your radar, that UFO would only be 1536 meters long! Your mind might well boggle at this point, but remember that you're simply viewing its dimensions relative to where you stand- not how big or small they actually are…It all comes down to relativity!
Time Dilation: What it Means
Because the speed of light is constant through space and time, it's relativity that comes into play when you use this principle. When we define the term- "the effect by which time slows down for a moving observer"- we have to remember that it happens relative to how fast another moving object approaches or recedes from us!
If one object was stationary in our frame of reference, though, it would appear as if nothing had changed with its appearance; This is because both objects are moving at the same rate (relative to each other), so no gravitational effects can occur.
Time dilates and contraction occurs when an object moves faster than c- The closer two objects get together, the slower they approach each other. And the opposite happens too: Objects recede from each other at the same rate, so time appears to pass faster for both objects.
Related Post: Why Should You, or Anyone Else Who Cares About Space Travel Should to Learn Physics?
This can be applied in many ways: For example, if I had a clock on Earth and another clock on a spaceship which was going 0.8c (in the opposite direction of course), we could compare how much time has passed between them since departure; According to the clocks, 7 days will have passed for me and only 5 days will have passed for my partner (relative to his frame of reference). We could even try it out with real clocks!
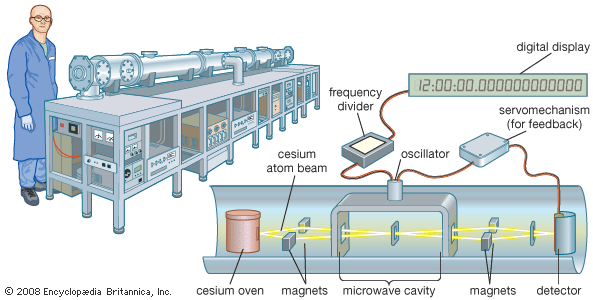
Scenario 1- Yes, this is possible! In fact, atomic clocks are routinely used now to test relativity through precise measurements of their behavior. But how would you go about doing it?
Let's say you took a clock from Earth and affixed it to the top of an airplane. Then, you allowed that plane to accelerate to 0.8c in the opposite direction. How would time behave compared to on earth?
The short answer is- we don't know! The problem lies with the realization that objects at superluminal velocities have not been measured yet (for obvious reasons), so there are no known experiments nor models which can accurately predict how much time would pass for both observers- only rough estimates.
However: Scenario 2- We can use computer modeling (at least) to give us more accurate results over what will happen if a spaceship approaches near light speed…For example: Since time dilation is dependent on the mass of the object (and how close it is to 0.8c), what will happen according to models if a certain spaceship reaches that velocity?

As you can see from this graph- which is derived from Einstein's equation for time dilation as a function of velocity, frequency and mass- when v = c, T = infinity! This means that movement at light speed would result in the existence of eternity for both observers; However, as soon as v decreases below c, T starts to approach zero again and soon returns to normal . If we want to know the quantitative behavior of time dilation in regards to an actual spaceship, though, we could solve this equation with some algebraic manipulation:
e0.8c is the time dilation for a frequency of c, and e0.6c is when time dilation is 40%. Integrating for both cases, we get: v2 = c2 + (1-e-μt/τ)2
where μ = reduced mass and τ= proper time Now that you have the equation above in terms of the given variables, it's easy to see how it will behave as v approaches infinity at light speed (!). Since T(v→∞) → ∞, then t → -∞! So if a spaceship can reach 0.8c or more, time appears to stop . In fact- if it reaches 0.999... c , all observers would be moving backwards in time!
The receding object paradox. While Einstein's theory of relativity has been able to explain many phenomena which we are familiar with today, there is still one major problem: As two objects approach each other, the closer they get together, the slower both of their proper times pass relative to each other.
Yet, if this happens when you and a spaceship (for example) get close enough to be within its light cone (the surface it can affect), then it means you're going faster than that object! So how does it maintain a constant velocity? And how would an observer on earth see this behavior?

According to Einstein's equations for length contraction and time dilation, as the distance between the two objects gets smaller and smaller, the slope of ds/dτ gets steeper and steeper (as it approaches ∞). Yet, when everything is at a constant velocity from each other, they should have the same value- so there must be something wrong with this equation! How could this behavior be explained?
Well, we know that the object would not really move faster than light speed relative to you. Instead- because its clock is moving very quickly compared to you (but slower than relativistic speeds due to length contraction), it appears to be moving more slowly as a result. This means that what actually happens is two different things:
The object in fact recedes from you at 10 light seconds per second... but since time passes for both of you at different rates, you see it as moving away from you slower- at 10c/μ seconds per second.
This means that if the object is 20 light moments away from you (where the proper time of both observers is equal), all of its progress only happens in 20μ seconds! Due to length contraction, this also causes it to appear smaller and smaller until it's infinitesimally small on your horizon too.
When two objects are close together like this, their observations can differ greatly: For example, let's say that due to the time dilation effect explained above, a nearby spaceship has an apparent velocity of -0.1c(t'=20). Since there is a difference between our velocities which is closer to zero, it means that our clocks will be moving relative to each other so fast that we'll see time slow down for the spaceship. Since its proper time has already changed (which is equal to ours when t'=0), then I can use my equations above to find out how its velocity appears... r=(v-√((v2/c2)-1)(t'-t))1/2
so v(t')=-0.0989 and -0.1029 at τ=20μs- or just 0.01c! So not only does it appear slower than you- but it's actually almost stopped! How does this paradox happen? Well, for one thing, there's no such thing as "the same velocity" when your times are different.
When two objects are traveling through space, they will always have slightly different velocities due to the fact that in order to stop time dilation from happening, an object can only be moving at relativistic speeds (or less).
Even if they're both going 0c relative to each other, one of them is still technically receding (and will appear larger on your horizon) because its clock is moving quickly!
This is why it's so difficult to maintain a constant speed in space, and why you cannot propose a spaceship which goes at the same speed for every observer: You must make sure that everybody sees it move with a constant velocity by slowing downtime for everybody who's moving slower!
In order to do this, you should be going as close to c as possible- but if you're too close (i.e. within your light cone), then time will move so slowly that it will take forever for another object to get there (like the spaceship in our example).
So why is this important? Well, it says that when two objects are at rest relative to each other, they can only experience length contraction and time dilation if their velocities differ from 0c by a factor of less than 1-(although they still see themselves as being at rest… which is not true ).
Related Post: Why Should You, or Anyone Else Who Cares About Space Travel Should to Learn Physics?

Yet, for one object to be able to have a "speed" even though it has no velocity, it must be moving between these two velocities, which is a very small fraction!
So does this mean that an object can move at speeds greater than c? Yes- but only in one direction (forward or backwards in time relative to you). If the object is heading toward us, then its clock will appear faster than yours; however, if it's moving away from us, then it will see us as having a slower clock.
For example, let's say that I have a spaceship that moves away from you at 0.1c (on your time dilation scale), and we're 33 light minutes apart. That means its clock is moving so fast that it's t'=20 seconds for me… but it's t'=2 years for the astronaut! So let's say he starts up his engine and goes full throttle, which causes him to move closer to us at 0.05c relative to us on our clocks (which will also cause him to appear smaller because of length contraction).
His new velocity is v=0.05*√((v2/c2)-1)(t'-t)=0.05×√(5-1)≈0.0732c , and t'=1 year for him so far. Since his clock is moving relatively faster on my horizon than his, it means that the time dilation effect has sped up my clock by a factor of √((v2/c2)-1)×t'-t =√(732-5), which is equal to 243.
This means that although he's still going 0.05c relative to me… he will appear to be slowing down!
If he turns around, the same thing happens. He'll now move away from us at -0.05c relative to us, causing him to appear slower yet (and for me to slow down even further).
This example is a bit confusing because I've shown you an object that's moving backward in time relative to us… but what would it look like if our spaceship moved toward each other?
That will be posted later on... but before that, I will go over another exciting aspect of relativity: length contraction! maybe tomorrow or Wednesday cause that is a broad topic.
If you enjoy this post as much as I enjoy writing them share your thought.. we love to read them or if you have any suggestions let me know.
Thanks for reading and Cheers!!
Reference and Image Source(some):



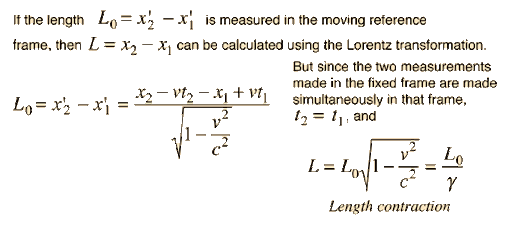






When i was 15 year old i was read about it in class 10th and today after 10 year i read once again with the help of your article thank you so much to share with us