Calculating the numerical value of Pi is an ancient mathematical challenge. In this article, I'll explain how it can be done via Monte Carlo simulations.
A Monte Carlo simulation is a numerical technique involving the generation of many random trials. It is widely employed in the fields of science and engineering, and can be used to solve a wide selection of problems. To introduce how it can be used to calculate Pi, consider a circle circumscribed by a square:
If you were to randomly throw arrows at this figure, how many of the arrows would you expect to get inside the circle? If your throw is completely random, the amount of arrows that would land in a given patch would be proportional to the area of the patch. If we compute the ratio of the circle's area to the square's area:
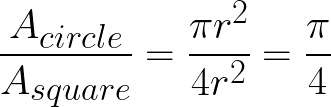
this ratio will give us the fraction of darts that land inside the circle. On a computer, we can virtually "throw darts" at the square, and compute this percentage. All you have to do is multiply by 4, and you will approximate pi better and better as the number of dart throws grows large!
At the heart of the Monte Carlo method is randomness, so we'll start by importing Python's built-in random library. Next, we decide how many darts we would like to throw - we'll arbitrarily set it to 100,000, since the calculation is cheap. Finally, we generate 100,000 random x coordinates between 0 and 1, along with 100,000 random y coordinates. If the point lies on the circle, we count it.
import random
n_trials = 100000
num_in = 0
for trial in range(n_trials):
# Generate a random x and y coordinate
rand_x = random.random()
rand_y = random.random()
# If the point lies within the circle, count it
if rand_x**2 + rand_y**2 < 1:
num_in += 1
approx = 4*(num_in/n_trials)
print("Pi Approximation: {}".format(approx))Using 100,000 random points, we arrive at the approximation: 3.14232. Not bad! Try the code for yourself, and see if you can get away with a smaller number of trials.
If you enjoyed learning about Monte Carlo, check out some of my GitHub projects that use this method:
2) Computing a definite integral
3) Estimating liquid properties
Thanks for reading!
